O Que É Razão E Proporção Exemplos –
O Que É Razão E Proporção Exemplos oferece uma jornada abrangente por esses conceitos fundamentais, explorando suas definições, tipos, propriedades e aplicações práticas. Prepare-se para mergulhar em um mundo de relações matemáticas que moldam nosso entendimento do mundo ao nosso redor.
Descubra a essência da razão, compreenda a relação entre razão e proporção e explore os diversos tipos de proporções, como direta, inversa e geométrica. As propriedades fundamentais das razões e proporções serão reveladas, ilustrando seu papel crucial em equações e resolução de problemas.
*
Conceito de Razão e Proporção

Para compreender o conceito de razão e proporção, é fundamental entender que esses dois conceitos estão intimamente ligados e representam relações matemáticas importantes.
A razão é uma comparação entre duas quantidades ou valores. É expressa como uma fração ou como dois pontos (:) e indica quantas vezes uma quantidade contém a outra. Por exemplo, se temos uma caixa com 12 maçãs vermelhas e 8 maçãs verdes, a razão de maçãs vermelhas para maçãs verdes é 12:8 ou 3:2.
Proporção
Uma proporção é uma igualdade entre duas razões. Em outras palavras, ela afirma que duas razões são iguais. Uma proporção é escrita como uma equação com dois pontos (:) no meio. Por exemplo, se temos uma receita que pede 2 xícaras de farinha para cada 1 xícara de açúcar, podemos escrever a proporção como 2:1.
Tipos de Razão e Proporção

As razões e proporções são ferramentas matemáticas que nos permitem comparar quantidades e identificar relacionamentos entre elas. Existem diferentes tipos de razões e proporções, cada uma com suas características e aplicações específicas.
Tipos de Razão
Uma razão é a comparação de duas quantidades ou medidas. Existem três tipos principais de razões:
- Razão Simples:Compara duas quantidades sem usar nenhuma unidade de medida. Por exemplo, a razão de meninos para meninas em uma sala de aula pode ser 3:4.
- Razão Composta:Compara duas razões. Por exemplo, se a razão de meninos para meninas em uma sala de aula é 3:4 e a razão de alunos para professores é 20:1, a razão composta é (3:4) : (20:1).
- Razão Contínua:Compara duas quantidades que podem variar continuamente. Por exemplo, a razão entre a distância percorrida por um carro e o tempo gasto pode ser expressa como uma razão contínua.
Tipos de Proporção
Uma proporção é uma equação que afirma que duas razões são iguais. Existem três tipos principais de proporções:
- Proporção Direta:Ocorre quando duas quantidades variam na mesma proporção. Por exemplo, se o número de horas trabalhadas é diretamente proporcional ao salário ganho, então a proporção entre o número de horas e o salário é constante.
- Proporção Inversa:Ocorre quando duas quantidades variam em proporções inversas. Por exemplo, se o tempo gasto para completar uma tarefa é inversamente proporcional ao número de pessoas trabalhando nela, então a proporção entre o tempo e o número de pessoas é constante.
- Proporção Geométrica:Ocorre quando a razão entre duas quantidades é constante e a razão entre duas quantidades sucessivas é a mesma. Por exemplo, se uma sequência de números é 2, 4, 8, 16, 32, então a proporção entre cada termo e o termo anterior é 2.
Propriedades de Razão e Proporção

As razões e proporções possuem propriedades fundamentais que orientam seu uso e aplicação em diversos contextos. Essas propriedades definem relacionamentos entre razões e proporções, permitindo operações e deduções lógicas.
Propriedades das Razões
As razões possuem as seguintes propriedades:
- Reflexiva:Toda razão é igual a si mesma (a/b = a/b).
- Simetria:Se a/b = c/d, então b/a = d/c.
- Transitiva:Se a/b = c/d e c/d = e/f, então a/b = e/f.
Propriedades das Proporções
As proporções possuem as seguintes propriedades:
- Produto Cruzado:Se a/b = c/d, então ad = bc.
- Inversa:Se a/b = c/d, então b/a = d/c.
- Aditiva:Se a/b = c/d e e/f = g/h, então (a + e)/(b + f) = (c + g)/(d + h).
Exemplos, O Que É Razão E Proporção Exemplos
Vamos ilustrar essas propriedades com alguns exemplos:
Propriedade Reflexiva:2/3 = 2/3
Propriedade Simetria:Se 3/4 = 6/8, então 4/3 = 8/6
Propriedade Transitiva:Se 1/2 = 2/4 e 2/4 = 3/6, então 1/2 = 3/6
Produto Cruzado:Se 5/6 = 10/12, então 5 x 12 = 6 x 10 (60 = 60)
Aplicações de Razão e Proporção
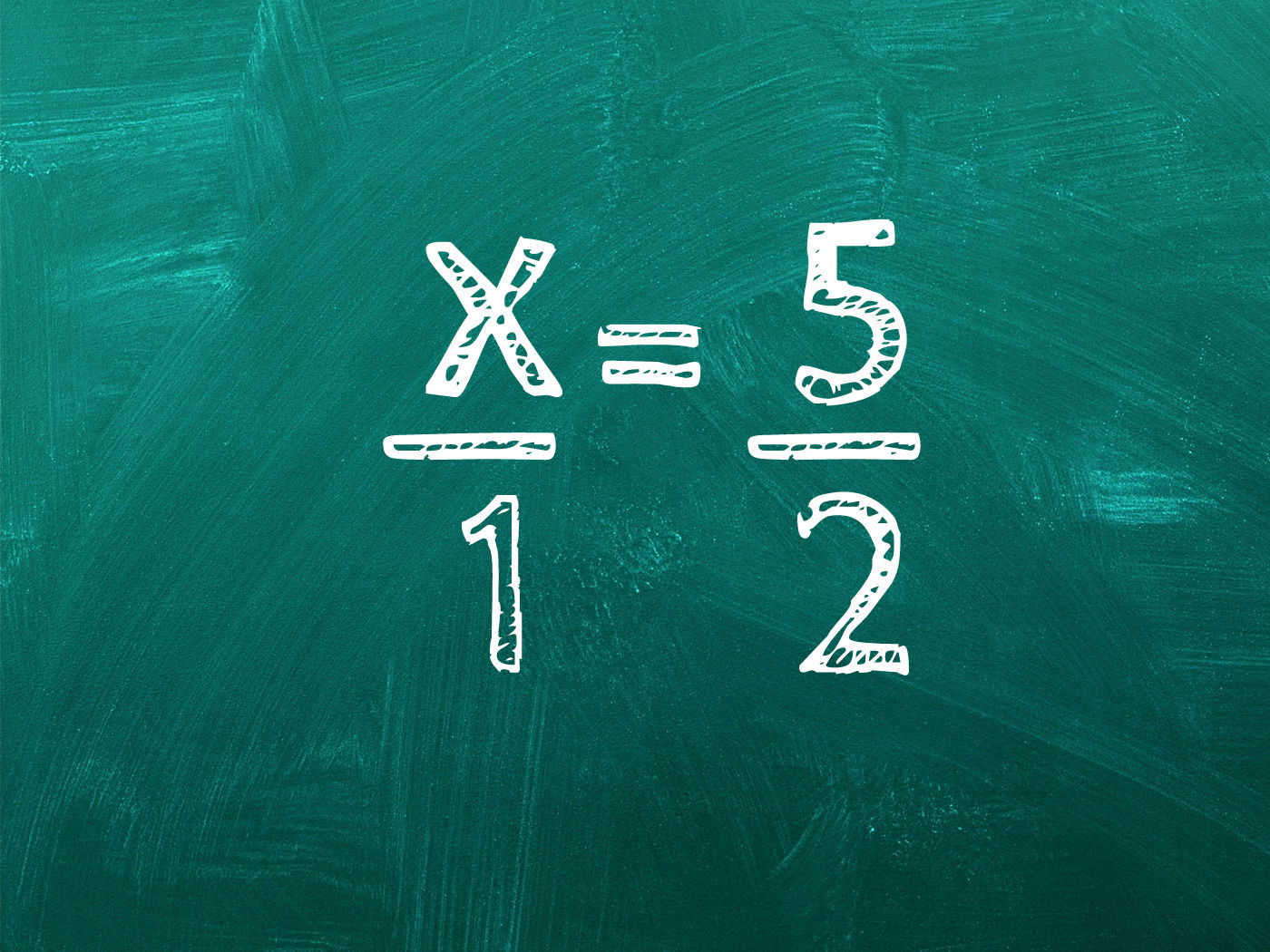
A razão e a proporção são conceitos matemáticos que encontram diversas aplicações práticas em diferentes áreas do conhecimento, como matemática, ciências e engenharia. Elas permitem estabelecer relações entre grandezas e resolver problemas envolvendo proporcionalidade.
Na tabela abaixo, apresentamos alguns exemplos específicos de como razão e proporção são usadas em contextos do mundo real:
Matemática
- Calcular o tamanho de um objeto em uma fotografia usando a proporção entre o tamanho real e o tamanho na fotografia.
- Resolver problemas de semelhança de triângulos usando a proporção entre os lados correspondentes.
- Encontrar a inclinação de uma reta usando a razão entre a diferença de ordenadas e a diferença de abscissas de dois pontos.
Ciências
- Calcular a concentração de uma solução usando a proporção entre a quantidade de soluto e a quantidade de solvente.
- Determinar a velocidade de um objeto usando a razão entre a distância percorrida e o tempo gasto.
- Converter unidades de medida usando proporções, como converter quilômetros em milhas ou libras em gramas.
Engenharia
- Projetar estruturas usando a proporção entre a carga e a resistência do material.
- Calcular a quantidade de materiais necessários para uma construção usando a proporção entre o volume do objeto e a densidade do material.
- Otimizar o desempenho de um sistema usando a proporção entre o custo e o benefício.
Exercícios e Problemas
Para aprimorar a compreensão de razões e proporções, é essencial praticar exercícios e resolver problemas. Esta seção apresenta uma série de exercícios para cálculo de razões e proporções, além de problemas resolvidos para ilustrar sua aplicação.
Os exercícios são graduados em dificuldade, começando com exemplos básicos e progredindo para problemas mais desafiadores. Os problemas resolvidos fornecem uma compreensão passo a passo da aplicação de razões e proporções em cenários do mundo real.
Exercícios
- Calcule a razão entre 12 e 18.
- Estabeleça a proporção entre 4 e 6.
- Determine se a razão 3:5 é equivalente à proporção 9:15.
Problemas Resolvidos
- Uma receita pede 2 xícaras de farinha para cada 3 xícaras de açúcar. Se você deseja fazer um bolo com 6 xícaras de açúcar, quantas xícaras de farinha serão necessárias?
- Um mapa tem escala de 1:50.000. Se a distância real entre duas cidades é de 200 km, qual será a distância entre as cidades no mapa?
Problemas de Desafio
| Problema | Dificuldade |
|---|---|
| Um investidor dividiu seu capital em três investimentos na proporção 2:3:5. Se o investimento total for de R$ 120.000,00, quanto foi investido em cada um? | Média |
| Um trem viaja a uma velocidade constante de 80 km/h. Se a distância entre duas estações é de 240 km, quanto tempo o trem levará para viajar entre as estações? | Avançada |
Concluímos nossa jornada com uma compreensão profunda de razão e proporção. Esses conceitos são ferramentas essenciais para desvendar padrões, fazer previsões e compreender fenômenos do mundo real. De cálculos científicos a obras de arte, a razão e a proporção moldam nossa percepção do mundo, tornando-as indispensáveis para o pensamento crítico e a resolução de problemas.
*
Essential FAQs: O Que É Razão E Proporção Exemplos
O que é razão?
Razão é a comparação entre duas quantidades do mesmo tipo, expressa como uma fração ou uma divisão.
Como a razão difere da proporção?
Uma proporção é uma igualdade entre duas razões, indicando que as quantidades estão relacionadas de forma proporcional.
Quais são os tipos de proporções?
Existem vários tipos de proporções, incluindo direta, inversa e geométrica, cada uma com suas características únicas.
-*

