Exemplo De Numeros Que Pertencem Ao Conjunto Dos Numeros Inteiros, é um conceito fundamental da matemática que abrange todos os números que podem ser representados na reta numérica, incluindo positivos, negativos e zero. Compreender os números inteiros é crucial para diversas áreas do conhecimento, desde as operações básicas até a resolução de problemas complexos em física, química e engenharia.
Neste contexto, exploraremos a definição dos números inteiros, suas propriedades e exemplos práticos que demonstram sua relevância na vida real. Mergulharemos nas operações matemáticas envolvendo esses números, incluindo adição, subtração, multiplicação e divisão, e desvendaremos as propriedades associativas, comutativas e distributivas que regem essas operações.
Introdução aos Números Inteiros
Os números inteiros são um conceito fundamental na matemática, representando um conjunto de números que inclui os números naturais (1, 2, 3, …), seus opostos negativos (-1, -2, -3, …) e o zero (0). Eles são essenciais para a compreensão de diversos conceitos matemáticos, desde a contagem e a medição até a álgebra e a análise.
Representação na Reta Numérica
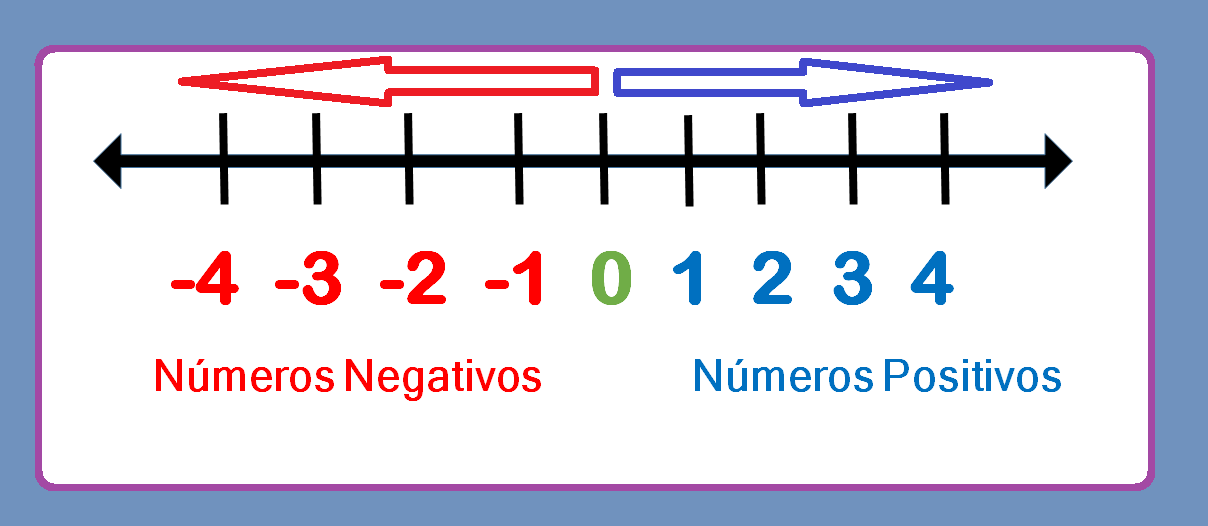
Os números inteiros podem ser representados na reta numérica, onde o zero é o ponto central, os números positivos ficam à direita do zero e os números negativos ficam à esquerda. Cada número inteiro ocupa um ponto específico na reta, e a distância entre dois números consecutivos é sempre a mesma.
Comparação com Outros Conjuntos Numéricos
Os números inteiros estão relacionados a outros conjuntos numéricos, como os números naturais, os números racionais e os números irracionais. Os números naturais são um subconjunto dos números inteiros, pois todos os números naturais são também números inteiros. Os números racionais são números que podem ser expressos como uma fração de dois números inteiros, e incluem os números inteiros como um caso especial.
Os números irracionais, por outro lado, não podem ser expressos como uma fração de dois números inteiros, como π e √2.
Propriedades dos Números Inteiros
Os números inteiros possuem propriedades específicas que os diferenciam de outros conjuntos numéricos. Essas propriedades facilitam a realização de operações matemáticas e a resolução de problemas que envolvem números inteiros.
Propriedades Básicas da Adição, Subtração, Multiplicação e Divisão
- Adição:A adição de números inteiros é comutativa (a + b = b + a) e associativa (a + (b + c) = (a + b) + c). A soma de um número inteiro com seu oposto é sempre zero (a + (-a) = 0).
- Subtração:A subtração de números inteiros é equivalente à adição do oposto do segundo número (a – b = a + (-b)).
- Multiplicação:A multiplicação de números inteiros é comutativa (a × b = b × a) e associativa (a × (b × c) = (a × b) × c). A multiplicação de um número inteiro por zero é sempre zero (a × 0 = 0), e a multiplicação de um número inteiro por 1 é sempre o próprio número (a × 1 = a).
- Divisão:A divisão de números inteiros é definida como a operação inversa da multiplicação. A divisão por zero é indefinida. A divisão de um número inteiro por 1 é sempre o próprio número (a ÷ 1 = a).
Propriedade da Ordem
Os números inteiros podem ser ordenados em uma sequência crescente ou decrescente. A propriedade da ordem permite comparar dois números inteiros e determinar qual é maior, menor ou igual ao outro. Por exemplo, 5 é maior que 3 (5 > 3), 3 é menor que 5 (3 < 5) e 5 é igual a 5 (5 = 5).
Valor Absoluto
O valor absoluto de um número inteiro é a sua distância do zero na reta numérica. Ele é sempre um número positivo ou zero. Por exemplo, o valor absoluto de 5 é 5 (|5| = 5) e o valor absoluto de -5 é também 5 (|-5| = 5).
Exemplos de Números Inteiros
Existem infinitos números inteiros, tanto positivos quanto negativos. Alguns exemplos de números inteiros são:
Tabela de Exemplos
| Número Inteiro | Tipo |
|---|---|
| -5 | Negativo |
| -3 | Negativo |
| -1 | Negativo |
| 0 | Zero |
| 1 | Positivo |
| 3 | Positivo |
| 5 | Positivo |
Ordem Crescente e Decrescente
Os números inteiros podem ser organizados em ordem crescente ou decrescente. A ordem crescente é do menor para o maior, enquanto a ordem decrescente é do maior para o menor. Por exemplo, os números inteiros da tabela acima, em ordem crescente, são: -5, -3, -1, 0, 1, 3, 5.
Em ordem decrescente, são: 5, 3, 1, 0, -1, -3, -5.
Números Inteiros em Diferentes Contextos
Os números inteiros são utilizados em diversos contextos do dia a dia, como:
- Temperatura:A temperatura pode ser expressa em graus Celsius ou Fahrenheit, que são números inteiros.
- Altitude:A altitude de um local em relação ao nível do mar é expressa em metros ou pés, que são números inteiros.
- Saldo Bancário:O saldo de uma conta bancária é expresso em unidades monetárias, que são números inteiros.
Aplicações dos Números Inteiros: Exemplo De Numeros Que Pertencem Ao Conjunto Dos Numeros Inteiros
Os números inteiros são ferramentas essenciais para resolver problemas em diversas áreas do conhecimento. Sua aplicação é fundamental para a compreensão de diversos fenômenos e para a realização de cálculos precisos.
Aplicações no Dia a Dia
- Contagem:Os números inteiros são utilizados para contar objetos, como pessoas, carros, livros, etc.
- Medidas:Os números inteiros são utilizados para medir grandezas, como comprimento, peso, tempo, etc.
- Cálculos Financeiros:Os números inteiros são utilizados para realizar cálculos financeiros, como o cálculo de juros, o pagamento de contas, etc.
Aplicações em Áreas Específicas
- Física:Os números inteiros são utilizados para representar grandezas físicas, como a massa, a velocidade, a aceleração, etc.
- Química:Os números inteiros são utilizados para representar o número de átomos em uma molécula, o número de elétrons em um átomo, etc.
- Engenharia:Os números inteiros são utilizados para realizar cálculos estruturais, projetar máquinas, etc.
Exemplo Prático
Imagine que você está organizando um evento e precisa comprar 100 cadeiras para acomodar os convidados. Você vai até uma loja e encontra cadeiras a R$ 50,00 cada. Para calcular o custo total das cadeiras, você multiplica o número de cadeiras (100) pelo preço unitário (R$ 50,00): 100 × 50 = 5000.
O custo total das cadeiras é R$ 5000,00, um número inteiro que representa o valor total da compra.
Operações com Números Inteiros
As operações básicas com números inteiros, como adição, subtração, multiplicação e divisão, são essenciais para a resolução de problemas matemáticos. Essas operações seguem regras específicas que permitem obter resultados precisos.
Exemplos de Operações
- Adição:5 + 3 = 8
- Subtração:7 – 2 = 5
- Multiplicação:4 × 6 = 24
- Divisão:12 ÷ 3 = 4
Propriedades Associativa, Comutativa e Distributiva
- Associativa:(a + b) + c = a + (b + c) e (a × b) × c = a × (b × c)
- Comutativa:a + b = b + a e a × b = b × a
- Distributiva:a × (b + c) = (a × b) + (a × c)
Resolução de Equações
As operações com números inteiros são utilizadas para resolver equações. Por exemplo, a equação 2x + 5 = 11 pode ser resolvida utilizando as operações básicas de adição e subtração. Subtraindo 5 de ambos os lados da equação, obtemos 2x = 6.
Dividindo ambos os lados por 2, obtemos x = 3. A solução da equação é x = 3, um número inteiro que satisfaz a equação original.
Ao final desta jornada, você terá uma compreensão sólida dos números inteiros, suas propriedades e aplicações. Aprofundar-se nesse conceito é essencial para dominar os fundamentos da matemática e expandir seus conhecimentos em áreas que exigem o uso de números inteiros.
Aproveite a oportunidade para explorar este universo numérico e fortalecer suas habilidades matemáticas!

