Funções Pares, Ímpares e Aquelas que Não São Nenhuma das Duas: Exemplo De Função Real Que Não É Par Nem Ímpar
Exemplo De Função Real Que Não É Par Nem Ímpar – Neste fio, vamos explorar o fascinante mundo das funções pares e ímpares, e, principalmente, as funções que não se encaixam em nenhuma dessas categorias. Vamos entender suas definições, propriedades, exemplos e aplicações práticas.
Definição de Funções Pares e Ímpares
Funções pares e ímpares são classificadas pela sua simetria em relação ao eixo y (par) e à origem (ímpar).
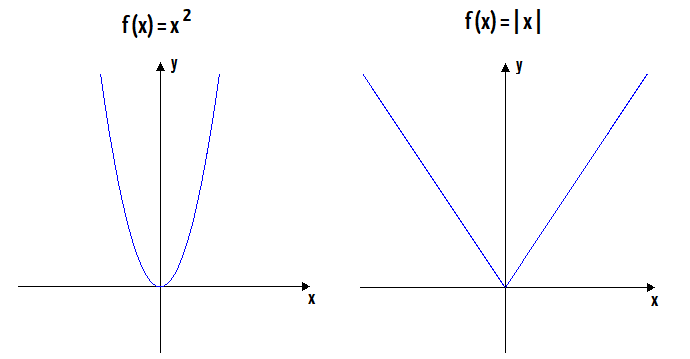
- Função Par: Uma função f(x) é par se, para todo x no seu domínio, f(-x) = f(x). Seu gráfico é simétrico em relação ao eixo y. Exemplo: f(x) = x². Se calcularmos f(-2) e f(2), ambos resultam em 4.
- Função Ímpar: Uma função f(x) é ímpar se, para todo x no seu domínio, f(-x) = -f(x). Seu gráfico é simétrico em relação à origem. Exemplo: f(x) = x³. Observe que f(-2) = -8 e f(2) = 8; um é o oposto do outro.
A principal diferença reside na simetria. Funções pares possuem simetria em relação ao eixo y, enquanto funções ímpares possuem simetria rotacional de 180 graus em torno da origem.
| Propriedade | Função Par | Função Ímpar | Exemplo |
|---|---|---|---|
| Definição | f(-x) = f(x) | f(-x) = -f(x) | – |
| Simetria | Eixo y | Origem | – |
| Gráfico | Simétrico em relação ao eixo y | Simétrico em relação à origem | – |
| Exemplo | f(x) = cos(x) | f(x) = sen(x) | f(x) = x² – x⁴ |
Exemplos de Funções Reais que Não São Pares Nem Ímpares, Exemplo De Função Real Que Não É Par Nem Ímpar
A maioria das funções não se encaixa perfeitamente nas categorias par ou ímpar. Vejamos alguns exemplos:
- f(x) = x + 1: f(-x) = -x + 1, que não é igual a f(x) nem a -f(x).
- f(x) = e^x: f(-x) = e^(-x) = 1/e^x, que não é igual a f(x) nem a -f(x).
- f(x) = x² + x: f(-x) = (-x)² + (-x) = x²
-x . Novamente, diferente de f(x) e -f(x).
Graficamente, essas funções não apresentam a simetria característica das funções pares ou ímpares. Por exemplo, o gráfico de f(x) = x + 1 é uma reta que não possui simetria em relação ao eixo y ou à origem.
Construção de Funções Não Pares Nem Ímpares
Um método simples para construir uma função que não seja par nem ímpar é combinar termos de funções pares e ímpares, ou usar funções que não possuem simetria intrínseca.
Exemplo: Começamos com uma função ímpar, g(x) = x³, e adicionamos uma função par, h(x) = x². A nova função f(x) = x³ + x² não será nem par nem ímpar, pois a soma de uma função par e uma ímpar, geralmente, resulta em uma função que não possui nenhuma das simetrias.
Propriedades de Funções Não Pares Nem Ímpares
Funções que não são pares nem ímpares não possuem as simetrias características, mas ainda assim exibem propriedades matemáticas interessantes.
- Ausência de Simetria: A propriedade mais óbvia é a ausência de simetria em relação ao eixo y ou à origem.
- Decomposição em partes par e ímpar: Qualquer função pode ser decomposta na soma de uma função par e uma função ímpar.
- Comportamento Geral: Seu comportamento gráfico é mais complexo e menos previsível do que o de funções pares ou ímpares.
Aplicações de Funções Não Pares Nem Ímpares
Muitas funções que modelam fenômenos reais não são nem pares nem ímpares. Um exemplo é a função que descreve o crescimento populacional de uma espécie. Diversos fatores podem influenciar o crescimento, resultando em uma curva que não apresenta simetria par ou ímpar.
Imagine uma função que modela a temperatura ao longo do dia. A temperatura sobe durante o dia e cai à noite, sem uma simetria clara em relação ao eixo y ou à origem. Uma função par ou ímpar não seria adequada para modelar essa situação de forma precisa.
Quais são as implicações práticas de estudar funções que não são pares nem ímpares?
O estudo dessas funções amplia nossa capacidade de modelar fenômenos reais que não exibem simetria par ou ímpar, abrindo caminho para soluções mais precisas em áreas como física, engenharia e ciência da computação.
Existe um método simples para verificar se uma função é par, ímpar ou nenhuma das duas?
Sim. Para verificar a paridade, avalie f(-x). Se f(-x) = f(x), a função é par. Se f(-x) = -f(x), a função é ímpar. Caso contrário, não é nem par nem ímpar.
Como as funções não pares nem ímpares se comportam em relação à integração e derivação?
As regras de integração e derivação se aplicam normalmente a essas funções, sem simplificações específicas decorrentes da falta de paridade, exigindo o uso das técnicas usuais de cálculo.

