Condição De Existência De Um Triângulo Exemplos – As Condições de Existência de Triângulos nos guiam pelo fascinante mundo da geometria, revelando as regras que determinam se um conjunto de segmentos de reta pode formar um triângulo válido. Vamos mergulhar nesta exploração, compreendendo as condições essenciais e os tipos de triângulos que elas permitem.
Para existir um triângulo, seus lados devem obedecer a certos critérios. A soma de quaisquer dois lados deve ser maior que o terceiro lado, e a diferença entre quaisquer dois lados deve ser menor que o terceiro lado. Essas condições garantem que os segmentos de reta possam formar um polígono fechado com três lados e três ângulos.
Condições de existência de um triângulo

Um triângulo é um polígono de três lados. Para que um triângulo exista, é necessário que a soma de quaisquer dois de seus lados seja maior que o terceiro lado.Exemplos de triângulos que satisfazem essas condições:* Triângulo equilátero: todos os lados são iguais.
Triângulo isósceles
dois lados são iguais.
Triângulo escaleno
todos os lados são diferentes.Com base nessas condições, podemos identificar os seguintes tipos de triângulos:* Triângulo acutângulo: todos os ângulos internos são menores que 90°.
Triângulo retângulo
um ângulo interno é igual a 90°.
Triângulo obtusângulo
um ângulo interno é maior que 90°.
Propriedades dos triângulos
Os triângulos são figuras geométricas que possuem três lados e três ângulos. Suas propriedades são importantes para resolver problemas geométricos e têm aplicações em diversas áreas, como arquitetura, engenharia e navegação.
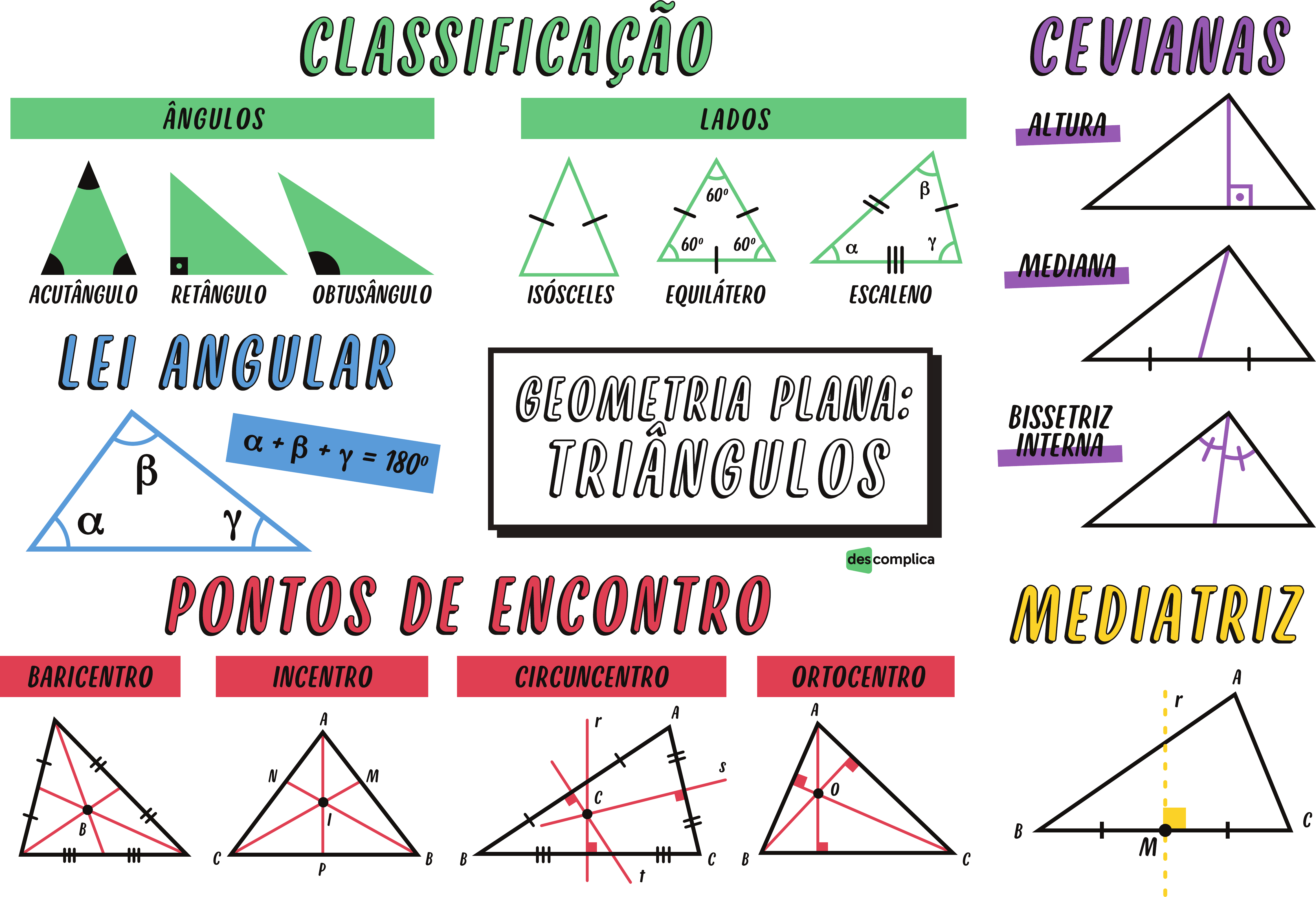
Ângulos dos triângulos
A soma dos ângulos internos de um triângulo é sempre 180 graus. Esta propriedade é conhecida como Teorema da Soma dos Ângulos Internos. Os triângulos podem ser classificados com base em seus ângulos:
- Triângulo acutângulo: todos os ângulos são menores que 90 graus.
- Triângulo retângulo: um ângulo é reto (90 graus).
- Triângulo obtusângulo: um ângulo é obtuso (maior que 90 graus).
Lados dos triângulos
Os lados de um triângulo podem ter diferentes comprimentos. Os triângulos podem ser classificados com base em seus lados:
- Triângulo equilátero: todos os lados têm o mesmo comprimento.
- Triângulo isósceles: dois lados têm o mesmo comprimento.
- Triângulo escaleno: todos os lados têm comprimentos diferentes.
Área dos triângulos
A área de um triângulo é dada pela fórmula: Área = (base – altura) / 2, onde base é o comprimento de um dos lados e altura é a distância perpendicular da base ao vértice oposto.
Exemplos de aplicação das propriedades dos triângulos
- Na construção, os triângulos são usados para determinar a estabilidade de estruturas.
- Na engenharia, os triângulos são usados para calcular forças e tensões em pontes e edifícios.
- Na navegação, os triângulos são usados para determinar a posição e direção de um navio.
Construção de triângulos: Condição De Existência De Um Triângulo Exemplos
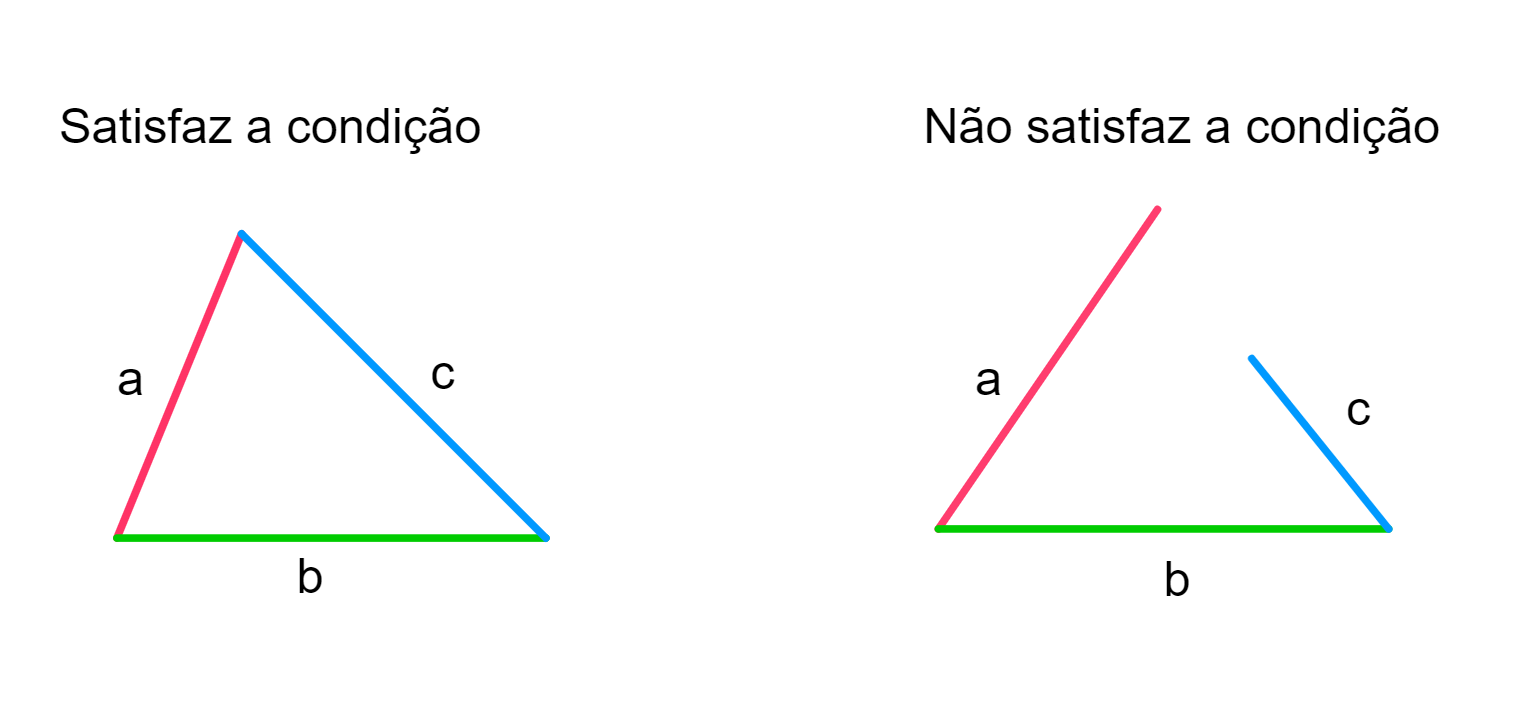
A construção de triângulos é uma habilidade fundamental em geometria. Existem vários métodos para construir triângulos usando régua e compasso. Nesta seção, demonstraremos esses métodos e forneceremos uma tabela resumindo os passos envolvidos.
Construção de triângulos com régua e compasso
Para construir um triângulo com régua e compasso, siga os passos abaixo:
- Use a régua para desenhar um segmento de reta.
- Use o compasso para marcar um ponto em um lado do segmento de reta.
- Abra o compasso até o comprimento do segmento de reta.
- Desenhe um arco a partir do ponto marcado em (2) que intercepte o outro lado do segmento de reta.
- Marque o ponto de intercepção do arco com o segmento de reta.
- Use a régua para conectar o ponto marcado em (2) ao ponto marcado em (5).
- Use a régua para conectar o ponto marcado em (5) ao ponto marcado em (1).
Tabela de métodos de construção de triângulos
A tabela abaixo resume os diferentes métodos de construção de triângulos e seus passos correspondentes:
| Método | Passos |
|---|---|
| Construção de triângulos com régua e compasso | Os passos descritos acima |
| Construção de triângulos com régua e transferidor | Use a régua para desenhar um segmento de reta. Use o transferidor para medir e marcar um ângulo em uma extremidade do segmento de reta. Use a régua para desenhar um segundo segmento de reta que forme o outro lado do ângulo. Use o transferidor para medir e marcar o ângulo restante no outro lado do segmento de reta. Use a régua para conectar as extremidades dos dois segmentos de reta para formar o triângulo. |
| Construção de triângulos com régua e esquadro | Use a régua para desenhar um segmento de reta. Use o esquadro para desenhar uma perpendicular ao segmento de reta em uma extremidade. Use a régua para desenhar um segundo segmento de reta que forme o outro lado da perpendicular. Use o esquadro para desenhar uma segunda perpendicular ao segmento de reta no outro lado do segmento de reta. Use a régua para conectar as extremidades dos dois segmentos de reta para formar o triângulo. |
Exemplos de construção de triângulos específicos
Aqui estão alguns exemplos de como construir triângulos específicos:
- Para construir um triângulo equilátero, use os passos descritos na seção anterior para construir um triângulo com todos os lados iguais.
- Para construir um triângulo isósceles, use os passos descritos na seção anterior para construir um triângulo com dois lados iguais.
- Para construir um triângulo retângulo, use os passos descritos na seção anterior para construir um triângulo com um ângulo reto (90 graus).
Teoremas relacionados a triângulos
Os teoremas relacionados a triângulos são fundamentais na geometria, fornecendo ferramentas para analisar e resolver problemas envolvendo essas formas. Esses teoremas estabelecem relacionamentos entre os lados, ângulos e áreas dos triângulos.
Teorema de Pitágoras
O Teorema de Pitágoras é um dos teoremas mais famosos e importantes da geometria. Ele afirma que em um triângulo retângulo, o quadrado do comprimento da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos comprimentos dos outros dois lados (os catetos).
a² + b² = c²
Onde:
- a e b são os comprimentos dos catetos
- c é o comprimento da hipotenusa
Teorema do Seno
O Teorema do Seno estabelece uma relação entre os comprimentos dos lados de um triângulo e os senos dos ângulos opostos a esses lados. Ele afirma que em qualquer triângulo:
a/sen(A) = b/sen(B) = c/sen(C)
Onde:
- a, b e c são os comprimentos dos lados
- A, B e C são os ângulos opostos aos lados
Teorema da Cosseno
O Teorema da Cosseno é uma generalização do Teorema de Pitágoras para triângulos não retângulos. Ele afirma que em qualquer triângulo:
c² = a² + b²
2abcos(C)
Onde:
- a, b e c são os comprimentos dos lados
- C é o ângulo oposto ao lado c
Esses teoremas são ferramentas poderosas para resolver problemas envolvendo triângulos. Eles podem ser usados para encontrar comprimentos de lados desconhecidos, ângulos e áreas, e também para determinar se um triângulo é retângulo ou não.
Aplicações de triângulos
Os triângulos são figuras geométricas versáteis com inúmeras aplicações práticas em vários campos. Eles desempenham um papel crucial em disciplinas como arquitetura, engenharia e navegação, permitindo que os profissionais resolvam problemas do mundo real e compreendam melhor o mundo físico.
Arquitetura
Em arquitetura, os triângulos são usados extensivamente por sua estabilidade e resistência. As estruturas triangulares, como telhados e vigas, podem suportar cargas pesadas e distribuir uniformemente o peso, garantindo a integridade estrutural dos edifícios. Além disso, os triângulos são usados para criar formas estéticas e dinâmicas, adicionando interesse visual e personalidade aos projetos arquitetônicos.
Engenharia, Condição De Existência De Um Triângulo Exemplos
Na engenharia, os triângulos são fundamentais para projetar e analisar estruturas complexas. Eles são usados em pontes, torres e outras construções para garantir estabilidade e resistência. Os princípios da trigonometria, baseados em triângulos, permitem que os engenheiros calculem forças, momentos e tensões, auxiliando na otimização de projetos e garantindo a segurança das estruturas.
Navegação
Na navegação, os triângulos são usados para determinar a localização e o curso de navios e aeronaves. A triangulação, uma técnica que usa medidas de ângulos em triângulos, permite que os navegadores calculem suas posições e estimem distâncias. Os triângulos também são usados em sistemas de orientação e navegação, como GPS e bússolas, para fornecer informações precisas sobre direção e localização.
Em resumo, as Condições de Existência de Triângulos fornecem as diretrizes cruciais para determinar se um conjunto de segmentos de reta pode formar um triângulo. Essas condições, juntamente com as propriedades e aplicações dos triângulos, formam a base da geometria, uma ferramenta essencial para entender o mundo ao nosso redor.
FAQs
O que são as Condições de Existência de Triângulos?
As Condições de Existência de Triângulos são regras que determinam se um conjunto de segmentos de reta pode formar um triângulo válido.
Quais são as Condições de Existência de Triângulos?
As condições são: a soma de quaisquer dois lados deve ser maior que o terceiro lado, e a diferença entre quaisquer dois lados deve ser menor que o terceiro lado.
Por que essas condições são importantes?
Essas condições garantem que os segmentos de reta possam formar um polígono fechado com três lados e três ângulos.


