Introdução ao Cilindro
Cilindro Tipos Partes Area Da Superficie Volume Exemplos Dd Calculos – O cilindro, uma forma geométrica tridimensional, é definido por duas bases circulares paralelas e congruentes, conectadas por uma superfície lateral curva. Sua presença na natureza e em objetos construídos pelo homem é vasta, desde árvores até edifícios, passando por peças mecânicas e recipientes de armazenamento. Compreender suas propriedades geométricas é fundamental em diversas áreas da ciência e engenharia.
Características Geométricas do Cilindro
Um cilindro é caracterizado por sua altura (distância entre as bases), o raio (distância do centro da base até qualquer ponto na circunferência), e a geratriz (segmento de reta que conecta pontos correspondentes nas duas bases). A área da superfície e o volume são propriedades diretamente relacionadas a essas dimensões.
Cilindro Reto e Cilindro Oblíquo
A principal distinção entre cilindros reside na relação entre suas bases e eixo. Num cilindro reto, o eixo é perpendicular às bases, resultando numa forma simétrica. Já no cilindro oblíquo, o eixo é inclinado em relação às bases, criando uma forma assimétrica. Um exemplo de cilindro reto é uma lata de refrigerante, enquanto um cone de trânsito inclinado pode ser visto como um exemplo de cilindro oblíquo, embora não seja um cilindro perfeito.
Importância do Cilindro em Ciência e Engenharia
O conceito de cilindro é crucial em diversas áreas. Na engenharia civil, o cálculo de volume e área de superfície é essencial no projeto de reservatórios, silos e tubulações. Na engenharia mecânica, cilindros são componentes fundamentais em motores, pistões e rolamentos. Em outras áreas, como arquitetura e design, a forma cilíndrica é explorada por sua estética e propriedades estruturais.
Tipos de Cilindros
Os cilindros podem ser classificados de acordo com a forma de suas bases e a relação entre o eixo e as bases. Esta classificação influencia diretamente no cálculo de suas propriedades geométricas.
Classificação e Diferenças entre Tipos de Cilindros
Existem diferentes tipos de cilindros, cada um com suas propriedades e aplicações específicas. A classificação mais comum considera a forma da base (circular ou elíptica) e a inclinação do eixo (reto ou oblíquo).
| Tipo | Características | Aplicações | Fórmula da Área da Superfície |
|---|---|---|---|
| Cilindro Reto Circular | Bases circulares, eixo perpendicular às bases. | Latas, tubos, pilhas. | 2πr² + 2πrh |
| Cilindro Oblíquo Circular | Bases circulares, eixo inclinado em relação às bases. | Componentes mecânicos complexos, alguns tipos de reservatórios. | Mais complexo, requer cálculo de integrais. |
| Cilindro Reto Elíptico | Bases elípticas, eixo perpendicular às bases. | Componentes de máquinas, estruturas arquitetônicas. | Mais complexo, envolve cálculo com semi-eixos maior e menor. |
| Cilindro Oblíquo Elíptico | Bases elípticas, eixo inclinado em relação às bases. | Situações especializadas em engenharia e arquitetura. | Cálculo bastante complexo, geralmente resolvido com métodos avançados de cálculo. |
Partes de um Cilindro
Para entender completamente as propriedades geométricas de um cilindro, é necessário conhecer suas partes constituintes e suas relações geométricas.
Componentes e Descrição Detalhada

- Base: Duas superfícies circulares congruentes e paralelas que formam as extremidades do cilindro. O raio da base (r) é a distância do centro da base até qualquer ponto na circunferência.
- Altura (h): A distância perpendicular entre as duas bases. No caso de um cilindro oblíquo, a altura é a distância mínima entre as bases.
- Raio (r): A distância do centro de cada base até qualquer ponto na circunferência da base.
- Geratriz: Segmento de reta que conecta pontos correspondentes nas duas bases. No cilindro reto, a geratriz é perpendicular às bases e igual à altura. No cilindro oblíquo, a geratriz é maior que a altura.
Área da Superfície de um Cilindro: Cilindro Tipos Partes Area Da Superficie Volume Exemplos Dd Calculos
A área da superfície de um cilindro é a soma da área das duas bases e da área da superfície lateral.
Cálculo da Área da Superfície Total de um Cilindro Reto
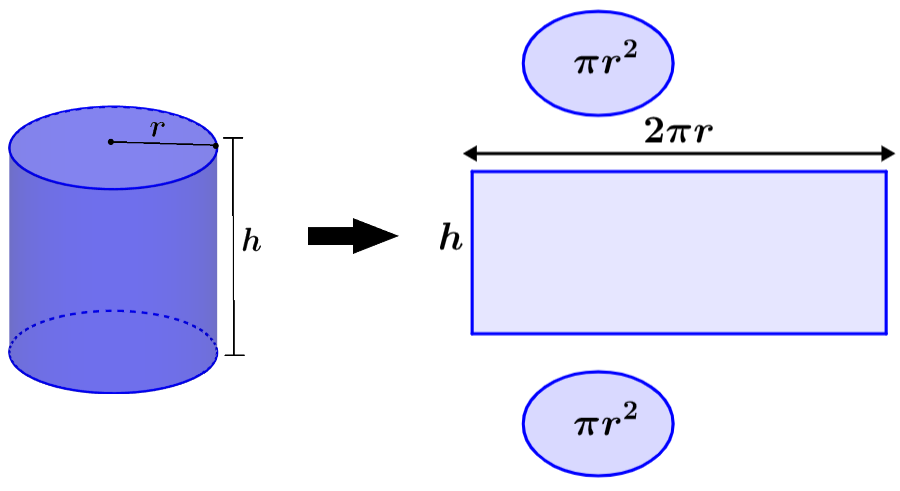
A fórmula para calcular a área da superfície total (A total) de um cilindro reto é: A total = 2πr² + 2πrh, onde ‘r’ é o raio e ‘h’ é a altura.
Cálculo da Área da Superfície Lateral de um Cilindro Reto
A área da superfície lateral (A lateral) de um cilindro reto é calculada por: A lateral = 2πrh. Exemplo: Para um cilindro com raio r = 5 cm e altura h = 10 cm, A lateral = 2π(5)(10) = 100π cm² ≈ 314,16 cm².
Comparação das Fórmulas para Cilindros Retos e Oblíquos, Cilindro Tipos Partes Area Da Superficie Volume Exemplos Dd Calculos
A fórmula para a área da superfície de um cilindro oblíquo é mais complexa e envolve cálculo integral, pois a geratriz não é perpendicular às bases. Para cilindros retos, a fórmula é direta e simples.
Volume de um Cilindro
O volume de um cilindro representa a quantidade de espaço que ele ocupa. Seu cálculo é fundamental em diversas aplicações práticas.
Fórmula para Calcular o Volume de um Cilindro Reto
O volume (V) de um cilindro reto é dado pela fórmula: V = πr²h, onde ‘r’ é o raio e ‘h’ é a altura.
Exemplos Práticos de Cálculo de Volume
| Raio (cm) | Altura (cm) | Volume (cm³) | Cálculo Detalhado |
|---|---|---|---|
| 5 | 10 | 250π ≈ 785,40 | V = π(5)²(10) = 250π |
| 2 | 7 | 28π ≈ 87,96 | V = π(2)²(7) = 28π |
| 10 | 15 | 1500π ≈ 4712,39 | V = π(10)²(15) = 1500π |
Aplicações do Cálculo de Volume em Situações Reais
O cálculo do volume de cilindros é essencial para determinar a capacidade de armazenamento de tanques cilíndricos, o volume de materiais em silos e o dimensionamento de tubulações em sistemas hidráulicos.
Exemplos e Aplicações de Cilindros
A forma cilíndrica está presente em inúmeros objetos e sistemas, demonstrando sua versatilidade e importância em diversas áreas.
Exemplos de Objetos do Cotidiano
- Lata de refrigerante (aprox. raio 3cm, altura 12cm)
- Rolo de papel toalha (aprox. raio 6cm, altura 20cm)
- Canudo (aprox. raio 0,5cm, altura 20cm)
- Pilar de concreto (aprox. raio 20cm, altura 300cm)
- Copo (aprox. raio 4cm, altura 10cm)
Aplicações em Diferentes Áreas
- Engenharia Civil: pilares, reservatórios de água, tubulações.
- Engenharia Mecânica: pistões, eixos, rolamentos.
- Arquitetura: colunas, torres, silos.
Aplicações em Setores Industriais

- Indústria alimentícia: embalagens, recipientes de armazenamento.
- Indústria automobilística: peças de motor, componentes de suspensão.
- Indústria têxtil: rolos de tecido, bobinas de fio.
Métodos de Cálculo para Cilindros
A determinação da área e volume de cilindros requer o uso de fórmulas e métodos específicos, dependendo do tipo de cilindro em questão.
Métodos para Calcular Área e Volume
Para cilindros retos, as fórmulas são relativamente simples, envolvendo o raio e a altura. Para cilindros oblíquos, métodos mais complexos, como o cálculo integral, podem ser necessários para obter resultados precisos.
Comparação de Métodos para Calcular Área da Superfície
O método mais comum para calcular a área da superfície de um cilindro reto é usar a fórmula 2πr² + 2πrh. Para cilindros oblíquos, a abordagem mais comum envolve o cálculo integral, que considera a variação da geratriz ao longo da superfície lateral.
Exemplo Prático de Cálculo de Volume de um Cilindro Oblíquo
O cálculo do volume de um cilindro oblíquo é mais complexo e geralmente envolve o uso de cálculo integral. Em casos simples, uma aproximação pode ser feita considerando um cilindro reto com altura equivalente à projeção da altura do cilindro oblíquo sobre o eixo perpendicular às bases.
Concluindo nossa exploração no mundo dos cilindros, fica claro a importância de dominar os conceitos de área e volume para uma vasta gama de aplicações práticas. Desde o projeto de estruturas complexas até o cálculo da capacidade de armazenamento de um tanque, a compreensão das fórmulas e dos métodos de cálculo é essencial. A versatilidade do cilindro, presente em objetos do cotidiano e em tecnologias avançadas, demonstra sua relevância na engenharia, na arquitetura e em inúmeras outras áreas.
Esperamos que esta análise tenha fornecido uma base sólida para futuras investigações e aplicações, permitindo que você aborde problemas relacionados a cilindros com confiança e precisão. A geometria, afinal, está presente em todos os lugares, e dominar seus princípios é fundamental para compreender o mundo que nos cerca.

