Introdução ao Cálculo de Determinantes: Calculos Do Determinantes De Uma Matriz Quadarda Definicoes Exemplos 4
Calculos Do Determinantes De Uma Matriz Quadarda Definicoes Exemplos 4 – O determinante é um valor escalar associado a uma matriz quadrada. Seu cálculo é fundamental em álgebra linear, fornecendo informações importantes sobre as propriedades da matriz e suas aplicações em diversos contextos matemáticos e científicos. Compreender o cálculo de determinantes é essencial para resolver sistemas de equações lineares, analisar transformações lineares, e calcular áreas e volumes em geometria analítica.
Definição de Determinante
O determinante de uma matriz quadrada A, denotado por det(A) ou |A|, é um número que pode ser calculado a partir dos elementos da matriz. A definição formal envolve o uso de permutações e seus sinais, mas métodos práticos de cálculo serão apresentados a seguir. Para matrizes de ordem 1, o determinante é o próprio elemento da matriz. Para matrizes de ordem superior, os métodos de cálculo variam, como veremos.
Importância do Cálculo de Determinantes
O cálculo de determinantes desempenha um papel crucial em diversas áreas da matemática e suas aplicações. Ele é essencial para determinar a invertibilidade de uma matriz (uma matriz é invertível se, e somente se, seu determinante é diferente de zero), resolver sistemas de equações lineares usando a regra de Cramer, calcular áreas e volumes de figuras geométricas, e analisar transformações lineares.
Em física, os determinantes são utilizados em mecânica, eletromagnetismo e outras áreas.
Propriedades Fundamentais dos Determinantes
Os determinantes possuem várias propriedades importantes que simplificam seu cálculo. Algumas das propriedades mais relevantes incluem: o determinante de uma matriz triangular (superior ou inferior) é o produto dos elementos da diagonal principal; o determinante de uma matriz é igual ao determinante de sua transposta; se multiplicarmos uma linha (ou coluna) de uma matriz por um escalar k, o determinante da matriz resultante é k vezes o determinante da matriz original; se trocarmos duas linhas (ou colunas) de uma matriz, o determinante muda de sinal.
Métodos de Cálculo para Matrizes 2×2 e 3×3
| Matriz | Método | Fórmula | Exemplo |
|---|---|---|---|
| 2×2 | Determinante Direto | ad – bc | Para a matriz
[ a b ]
[ c d ]
o determinante é ad – bc. Exemplo:
[ 2 3 ]
[ 1 4 ]
Determinante = (2*4) |
| 3×3 | Regra de Sarrus | Soma dos produtos das diagonais principais menos a soma dos produtos das diagonais secundárias. | Para uma matriz 3×3, a regra de Sarrus é visualmente mais fácil. Exemplo:
[ 1 2 3 ]
[ 4 5 6 ]
[ 7 8 9 ]
Determinante = (1*5*9 + 2*6*7 + 3*4*8) |
| 3×3 | Expansão de Cofatores | Escolha uma linha ou coluna. Para cada elemento, multiplique-o pelo seu cofator e some os resultados. | Utilizando a mesma matriz acima, a expansão por cofatores envolve cálculos mais complexos, mas o resultado é o mesmo (0). |
Expansão de Cofatores para Matrizes de Ordem Superior
A expansão de cofatores é um método geral para calcular o determinante de matrizes quadradas de qualquer ordem. Este método é baseado no conceito de cofator e menor complementar.
Conceito de Cofator e Menor Complementar
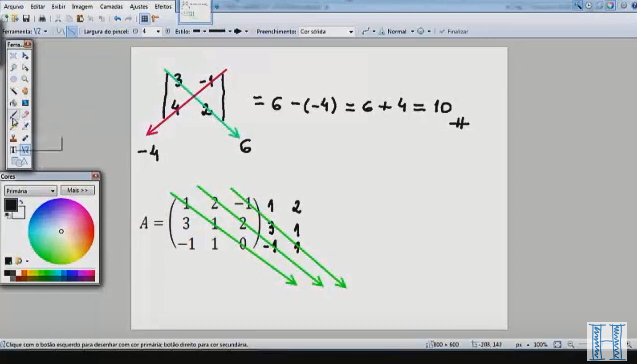
O menor complementar de um elemento a ij de uma matriz A é o determinante da submatriz obtida ao remover a i-ésima linha e a j-ésima coluna de A. O cofator de a ij é o menor complementar multiplicado por (-1) i+j.
Processo de Cálculo do Determinante usando Expansão de Cofatores
Para calcular o determinante de uma matriz nxn usando a expansão de cofatores, escolhe-se uma linha ou coluna. Para cada elemento da linha ou coluna escolhida, calcula-se o seu cofator e multiplica-se pelo elemento. A soma desses produtos resulta no determinante.
Exemplo de Cálculo do Determinante de uma Matriz 4×4
Para uma matriz 4×4, a expansão de cofatores envolve calcular quatro determinantes 3×3. Cada um desses determinantes 3×3 pode ser calculado usando a regra de Sarrus ou novamente por expansão de cofatores. O processo é iterativo, reduzindo a ordem da matriz até chegar a determinantes 2×2 ou 1×1.
Passos da Expansão de Cofatores para uma Matriz nxn
- Escolha uma linha ou coluna da matriz.
- Para cada elemento da linha ou coluna escolhida:
- Calcule o menor complementar (determinante da submatriz).
- Calcule o cofator (menor complementar
(-1)i+j).
- Multiplique o elemento pelo seu cofator.
- Some os resultados obtidos em cada passo.
Aplicações dos Determinantes, Calculos Do Determinantes De Uma Matriz Quadarda Definicoes Exemplos 4
Os determinantes possuem diversas aplicações práticas em diferentes áreas.
Aplicações em Geometria Analítica e Física
Em geometria analítica, o determinante é usado para calcular a área de um paralelogramo definido por dois vetores ou o volume de um paralelepípedo definido por três vetores. Em física, os determinantes são utilizados para resolver sistemas de equações lineares que descrevem fenômenos físicos, como no cálculo de forças e campos em mecânica e eletromagnetismo.
Determinante e Invertibilidade de uma Matriz
Uma matriz quadrada é invertível se, e somente se, seu determinante é diferente de zero. O determinante igual a zero indica que a matriz é singular e não possui inversa.
Determinante no Cálculo de Áreas e Volumes
O valor absoluto do determinante de uma matriz formada pelos vetores que definem um paralelogramo (2×2) ou um paralelepípedo (3×3) representa a área ou o volume da figura geométrica, respectivamente.
Determinante e Solução Única de Sistemas de Equações Lineares
Um sistema de equações lineares possui uma única solução se, e somente se, o determinante da matriz dos coeficientes é diferente de zero. Se o determinante for zero, o sistema pode não ter solução ou ter infinitas soluções.
Exemplos e Exercícios
A seguir, são apresentados exemplos de cálculo de determinantes para matrizes de diferentes ordens, utilizando diferentes métodos.
| Matriz | Método | Cálculo Passo a Passo | Resultado |
|---|---|---|---|
[ 1 2 ]
[ 3 4 ]
|
Determinante Direto | (1*4) -(2*3) = -2 |
-2 |
[ 1 2 3 ]
[ 4 5 6 ]
[ 7 8 9 ]
|
Regra de Sarrus | (1*5*9 + 2*6*7 + 3*4*8) -(3*5*7 + 2*4*9 + 1*6*8) = 0 |
0 |
[ 1 0 0 0 ]
[ 2 3 0 0 ]
[ 4 5 6 0 ]
[ 7 8 9 10 ]
|
Expansão de Cofatores | Como é uma matriz triangular inferior, o determinante é o produto dos elementos da diagonal principal: 1*3*6*10 = 180 | 180 |
[ 2 1 0 3 ]
[ 1 0 2 1 ]
[ 0 1 1 2 ]
[ 3 2 1 0 ]
|
Expansão de Cofatores | Este cálculo é extenso e requer expansão sucessiva de cofatores para matrizes 3×3, 2×2 e 1×1. O resultado final seria um número, cujo cálculo detalhado exigiria um espaço considerável. | (Resultado numérico após cálculo completo) |
Exemplo de Aplicação Prática
Um exemplo de aplicação prática é determinar se um sistema de equações lineares possui solução única. Se o determinante da matriz dos coeficientes for diferente de zero, o sistema tem solução única.
Caso contrário, o sistema pode ter infinitas soluções ou nenhuma solução.
Exercício: Resolução de Sistema de Equações Lineares usando Determinante
Resolva o sistema de equações lineares abaixo usando a regra de Cramer:
2x + y = 5 x - 3y = -8
Quais são as principais dificuldades encontradas pelos estudantes ao calcular determinantes?
As principais dificuldades residem na compreensão dos conceitos de cofator e menor complementar, na aplicação correta da regra de Sarrus e na expansão de cofatores para matrizes de ordem superior. A falta de prática e a ausência de exemplos concretos também contribuem para a dificuldade.
Existe um limite para o tamanho da matriz cujo determinante pode ser calculado?
Teoricamente, não há limite de tamanho. No entanto, o cálculo manual torna-se impraticável para matrizes muito grandes. Algoritmos computacionais são necessários para matrizes de alta ordem.
Como o determinante de uma matriz se relaciona com o seu posto?
Uma matriz quadrada é invertível (tem posto máximo) se, e somente se, seu determinante é diferente de zero. Um determinante nulo indica que a matriz é singular (tem posto menor que a sua ordem).

